About Kings, Mathematicians and our Logo
Welcome to your journey of the mind
About the life of Leonardo da Pisa
Fibonacci Sequences
About the logo
Literature
Welcome to your journey of the mind
It is a special pleasure for me to be the author of our first article. An exciting time and a new way lie ahead of us. This article was written in order to provide information about our concept (with special regard to our logo) and to give an insight into the conception and thoughts behind the corporate identity of Markus Vogl {Business & Data Science}.
Let us invite you to a short historical and mathematical journey and be inspired to reflect, to reread our sources and to study mathematics and the historical background. This is a homage to the life and work of Leonardo da Pisa (also known as Fibonacci). Our concept (and especially the creation of our logo) could not have been realized without his spiritual greatness.
About the life of Leonardo da Pisa

Regarding the influence of his work,there is far less known about the life of Leonardo da Pisa (Fibonacci) as one might have wished for. As a son of the warden of the Pisan trade colony in Bugia (Algeria), Leonardo da Pisa was born sometime around 1170 and is believed to have died around 1240 in Pisa (ETH-Bibliothek). During his journeys to Algeria as well as during several trips to the Orient, his muslim teachers taught him about the Hindu-Arabic numeral system. After his return to Pisa in the year 1200, he published the "Liber Abaci" in 1202 (an arithmetic book about calculation methods based on the Hindu-Arabic numeral system), which is a fundamental work of the epoch and for modern mathematics (ETH-Bibliothek). The works of Al-Khwarizmi (an Arabian mathematician of the 9th century and "eponym" of the term "Algorithm") and Abu Kamil (Egyptian mathematician of the 9th century and "eponym" of the term "Algebra") as well as those of acient scholars like Euklid and Ptolemaios have had a major influence on the work and thoughts of Leonardo da Pisa (ETH-Bibliothek).
By publishing the "Liber Abaci" as well as the monetary development towards cashless payment options, the dispute between the so called "Abacists" and a group called "Algorists" has been resolved in favor of the "Algorists" (ETH-Bibliothek). This incident resulted in the expansion of the today well known number system througout Europe.
Only a few years after the publication in 1226, Fibonacci met the emperor Friedrich II on the advice of the imperial philosopher Theodor of Antiochia. In contrast to some illiterate emperors, he showed great devotion and interest in science (Rader 2010). The court mathematician Johannes of Palermo immediately engaged Leonardo da Pisa in order to find solutions to some very complex mathematical challenges, which have been published in "Flos" and "Liber Quadrotorum". These works brought Friedrich II. closer to the scientific centres of the time, like those of Alfons X. el Sabio of Spain, son of Saint Ferdinand and grandchild of Phillipp of Swabia (Rader 2010).
The "Fibonacci Sequence" which became well known because of the challenge of "Fibonacci's Rabbits" was given its name by François Édouard Anatole Lucas in 1877, who named it after Fibonacci (ETH-Bibliothek). The work of Leonardo da Pisa had significant historical influence which can still be noticed in todays modern and highly technological world. A short outline of the influence during the Renaissance period as well as during the 18th and 19th century is provided in the following picture gallery (ETH-Bibliothek; Rader 2010):













Today the work and insights of Leonardo da Pisa did not only take a hold in science, but can also be found in Graphic Design and Finance (e.g. Elliot-Wave-Theory, Fibonacci-Retracements) (Roller 2015).
Fibonacci Sequences
Despite the major impact of Leonardo da Pisa and his work on modern science, the most known concept (either formal or graphical) is the so called Fibonacci Sequence. The Fibonacci Sequence is a mathematical sequence of non negative integers - with exception of the first two elements- which follow a recursive generating process (Roller 2015).
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, … are the first few elements of the Fibonacci Sequence. Every included element of the sequence (with exception of the first two numbers) is defined as the sum of the previous elements. The n th Fibonacci number can be labeled as f_{n} and be defined as follows (Walser 2012):
f_{n}= \begin{cases} 0 & \text{ for } n = 0 \\ 1 & \text{ for } n \in \left \{ 1, 2 \right \}\\ f_{n-1}+f_{n-2} & \text{ for } n \geq 3 \end{cases}
Extensions of this sequence regarding negative indices are the general basis for applications in various fields and research areas (e.g. generalizations regarding complex numbers, profinite numbers, vector spaces) and can be visualized as (Walser 2012):
f_{0}= 0
f_{-n}= \left ( -1 \right )^{n+1}f_{n}
Hereinafter, we consider the concept of divisibility as well as the commonly known term of the golden ratio, which is often associated with the abovementioned Fibonacci Sequence. Regarding the divisibilities of the elements and the relation with the indices of the sequence, it can be shown that an element equates an even number if the referring index is divisible by 3 (Vorob'ev 2013). The following table states (not completed) the divisibilities of the sequence
The table can be described by imagining the divisibility of an element being represented by its respective number provided that the number of the index is divisible by the same number (e.g. a number of the Fibonacci Sequence is divisible by 3 if the index is divisible by 4) (Vorob'ev 2013).
| Divisibility Element | Divisibility Index |
|---|---|
| 3 | 4 |
| 4 | 6 |
| 5 | 5 |
| 7 | 8 |
| 16 | 12 |
If one digs deeper into the concept of divisibility, it seems to be evident to take a deeper look into the behaviour of the elements among each other. Regarding the relations between an element in comparison to its nearest smaller element, it shows, that for the ratio \frac{f_{n}}{f_{n-1}} a treshhold value exists, which can be defined as (Walser 2012):
\varphi = \lim_{n \to \infty }\frac{f_{n-1}}{f_{n}}
This treshhold can be defined as the ratio between an element and its nearest smaller element and converges towards 0,6180… (Roller 2015).
Yet it is absolutely possible to define a treshhold which equates the ratio between an element and its nearest greater element, which converges towards 1,6180... and therefore converges towards the value labeled by Johannes Kepler , namely the golden ratio (Roller 2015):
\Phi = \lim_{n \to \infty }\frac{f_{n+1}}{f_{n}}
Some interesting properties worth mentioning are that \varphi is the reciprocal of \Phi and that the treshhold value doubles (or halves) regarding the ratios referring to the second following elements (Roller 2015).
Since the basic properties and the concept of divisibility of the Fibonacci Sequence are described, we can lay focus on the idea of Identities which are only briefly outlined before our journey contributes to a greater understanding (Walser 2012):




Identities of the Fibonacci Sequence
- \large f_{m+n}=f_{n+1}f_{m}+f_{n}f_{m-1}
- \large f_{m+n}=f_{n}L_{m}+\left ( -1 \right )^{m+1}f_{n-m} while
\large L_{m}=f_{m+1}+f_{m-1}=\Phi^{m}+\Psi ^{m} is defined as the Lucas Identitity - f_{n}^{2}-f_{n+k}+f_{n-k}=\left ( -1 \right )^{n-k}f_{k}^{2} describes the Identity of Cassini
- f_{m}f_{n-1}-f_{n}f_{m+1}=\left ( -1 \right )^{n}f_{m-n} states the Identity of d'Ocagne
As promised, we will reflect upon some exciting and noteworthy insights about the usability and possible applications of the Fibonacci Sequence. It is worth to emphasize the Belgian amateur mathematician Edouard Zeckendorf (1901-1983) and his so called Zeckendorf Theorem (Knuth 1968).
The theorem states, that each integer n > 0 can be uniquely be defined as sum of distinct, non succeding elements of the Fibonacci Sequence f_{j} (Knuth 1968). Therefore, a sequence \left ( c_{j} \right )_{i=0}^{k} of distinct, ascending elements exists in a manner that c_{j}\geq 2 and c_{j+1}> c_{j}+1 for j\geq 2 and n = \sum_{j=0}^{k}f_{c_{j}} holds (Knuth 1968).
To diminish the abstract character of the abovementioned argumentation, one should visualize the illustrative number n = 3 which can be described by the Zeckendorf theorem by using the declaration of the function f_{2+2} (Knuth 1968).
The description above explains how to define integers by using the properties of the Fibonacci Sequence. In the following, we will elucidate the generating process which was already known by Leonhard Euler and Daniel Bernoulli (who later in time provided mathematical proof). The generating process of Abraham de Moivre and Jacques Phillippe Marie Binet can be used to directly calculate the elements of the sequence (Walser 2012). Written as a matrix, the procedure can be formally described as (Walser 2012):
F = \left (\begin{matrix} 1 &1 \\ 1 & 0 \end{matrix} \right )^{n} = \left ( \begin{matrix} f_{n+1} & f_{n}\\ f_{n}& f_{n-1} \end{matrix} \right )
It is worth to highlight the Eigenvalue of F in particular, because it equals the golden ratio and its reciprocal leads to the deviation of the abovementioned formulation of Binet (Walser 2012).
The presented concepts may seem theoretical and abstract, but they do have practical indications as well. Besides Biology, Physics and other natural science disciplines as well as in Finance, these insights also take an important part in Computer Sciences (Knuth 1968). Fibonacci-Trees (also called AVL-Trees) as well as Fibonacci-Heaps (a special case of AVL-Trees) are worth to be mentioned at this point (Fredman und Tarjan 1987).
About the logo
After having discussed Leonardo da Pisa and the mathematical implications of his work, it is time to elucidate its relation with our logo, which is surely not straightforward. We would like to take the opportunity to give you a proper explanation of our logo and its design steps. Therefore, we would like to offer a deeper insight into Markus Vogl {Business & Data Science}.

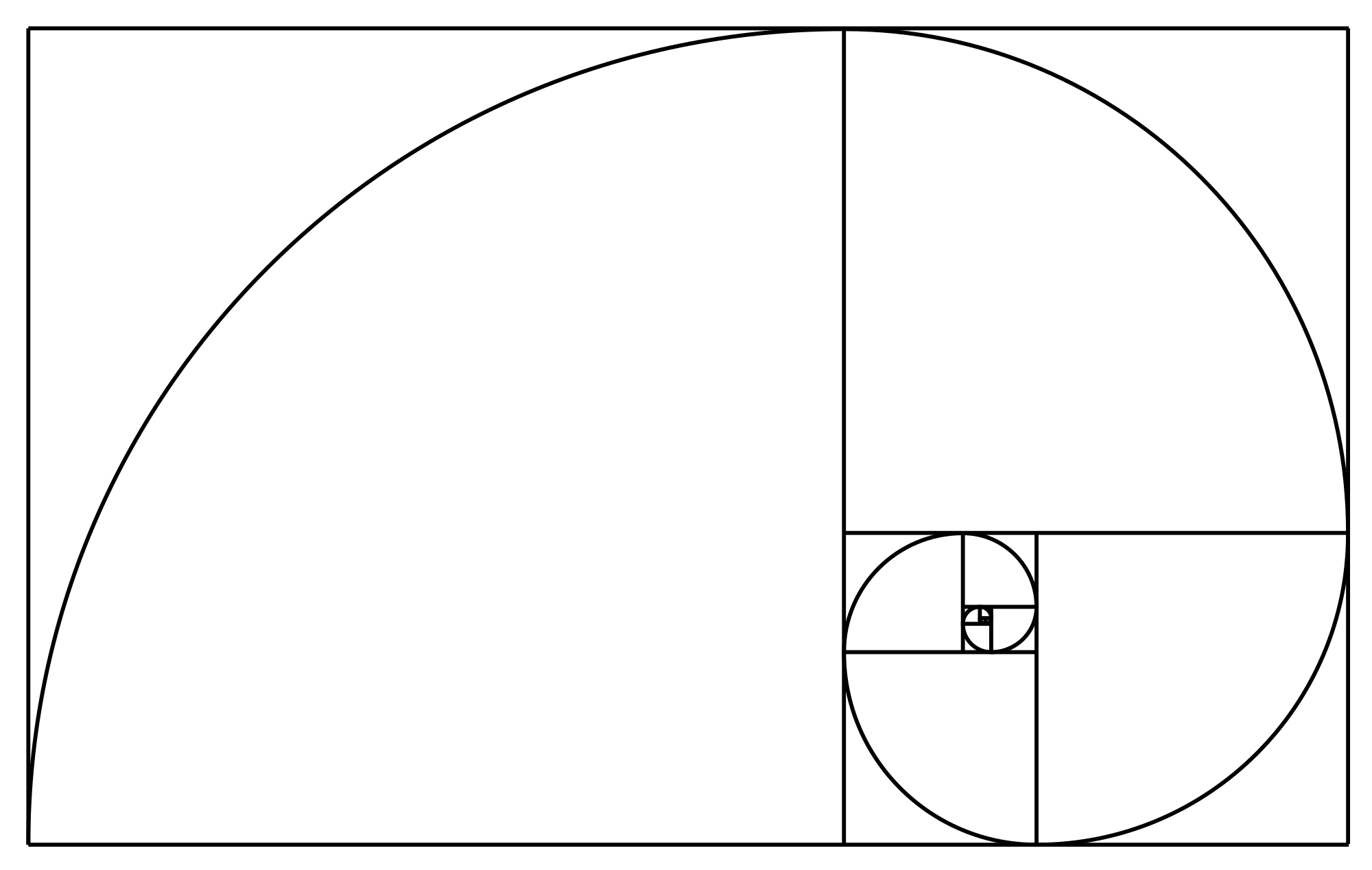
In the following section we demonstrate how the Fibonacci Spiral and the construction grid (righthand side) are used to design our logo (lefthand side). The construction grid visualizes the Fibonacci Sequence by matching the side lengths of the squares and the values of the elements of the sequence. The spiral is the graphical representation of the golden ratio.
For the logo, the inner circles of the squares labeled by the values 13 and 21 of the elements of the Fibonacci Sequence along with the square represented by the value 21 of the sequence are used (marked in orange). These three graphical elements become centralized.
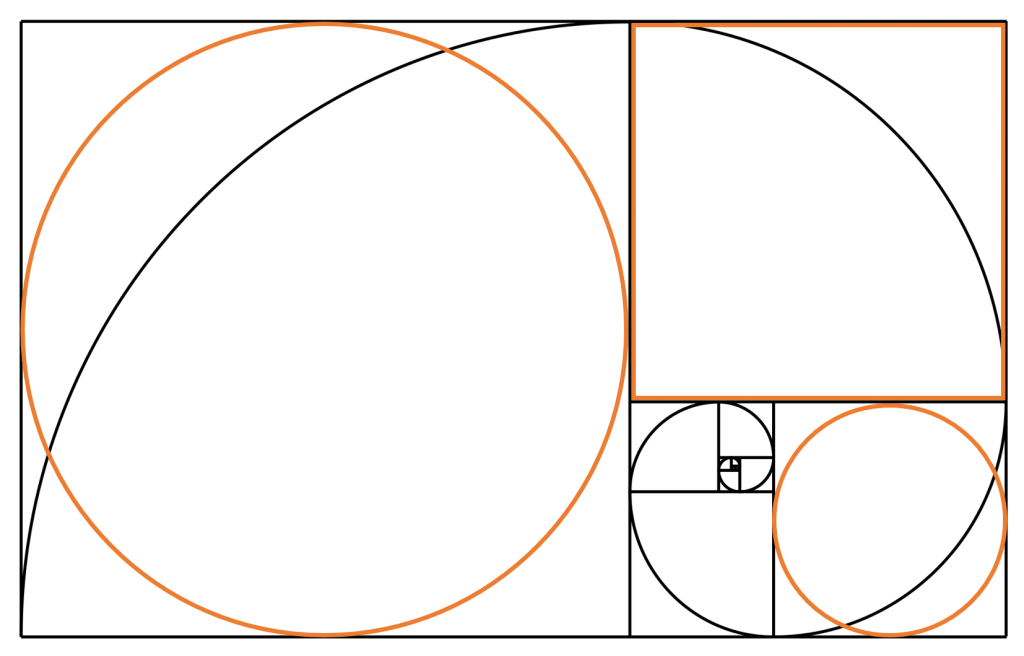

To complete the logo construction, straight lines between the intersection of the centre line (dotted line) and the inner square with the angles of the inner squares are inserted. Afterwards, these lines are duplicated and shifted towards the intersection of the central line and the outer circle.

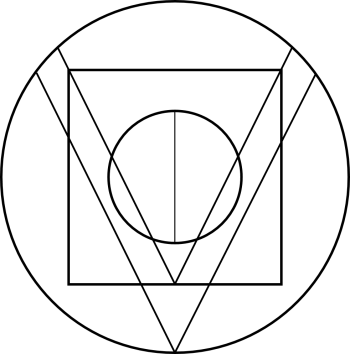
The logo, that is hereby created, allows scope for interpretation to discover new paths and patterns. It does not only represent our project, but should be considered as a source of joy and inspiration. Some possible ways of interpretation and meaning will be provided hereinafter.
The logo is a dedication to the artist George Phillips Odom, Jr. (1941-2010) and his works related to the golden ratio. In addition, the logo reflects the initials/the name M.Vogl of Markus Vogl {Business & Data Science}. We achieved both (marked in red), including a real picture of a "Vogel" (Pun intended, "Vogel" is the German word for "bird", the name "Vogl" misses the "e").




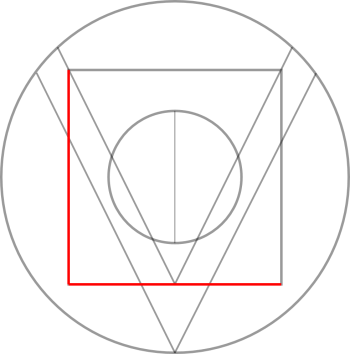
With this in mind, I am looking forward to your opinions, messages, ideas and future projects.
Yours Respectfully,
Markus Vogl
Literature
Benavoli, A.; Chisci, L.; Farina, A. (2009): Fibonacci sequence, golden section, Kalman filter and optimal control. In: Signal Processing 89 (8), S. 1483–1488. DOI: 10.1016/j.sigpro.2009.02.003.
ETH-Bibliothek: Biographie von Leonardo Pisano / Fibonacci. Un ponte sul Mediterraneo / Virtuelle Ausstellungen / ms / Home – ETH-Bibliothek. Online verfügbar unter http://www.library.ethz.ch/ms/Virtuelle-Ausstellungen/Fibonacci.-Un-ponte-sul-Mediterraneo/Biographie-von-Leonardo-Pisano, zuletzt geprüft am 26.12.2018.
Fibonacci-Analyse und Fibonacci-Trading: Die Know-how-Serie! Online verfügbar unter https://www.godmode-trader.de/know-how/fibonacci-analyse-und-fibonacci-trading-die-know-how-serie,5808764, zuletzt geprüft am 26.12.2018.
Fredman, Michael L.; Tarjan, Robert Endre (1987): Fibonacci heaps and their uses in improved network optimization algorithms. In: J. ACM 34 (3), S. 596–615. DOI: 10.1145/28869.28874.
Knuth, Donald Ervin (1968): The art of computer programming. Reading, Mass.: Addison-Wesley (Addison-Wesley series in computer science and information processing).
Ozturk, Selcuk; Yalta, Kenan; Yetkin, Ertan (2016): Golden ratio: A subtle regulator in our body and cardiovascular system? In: International journal of cardiology 223, S. 143–145. DOI: 10.1016/j.ijcard.2016.08.147.
Rader, O. B. (2010): Friedrich II.: der Sizilianer auf dem Kaiserthron : eine Biographie: Beck. Online verfügbar unter https://books.google.de/books?id=14iWw9uYFHwC.
Roller, K. (2015): Ichimoku-Trading: Besser traden mit der Wolkenchart-Indikatortechnik: FinanzBuch Verlag. Online verfügbar unter https://books.google.de/books?id=RyzfCQAAQBAJ.
Vorob’ev, Nikolai Nikolaevich (2013): Fibonacci Numbers. Newburyport: Dover Publications (Dover Books on Mathematics). Online verfügbar unter http://gbv.eblib.com/patron/FullRecord.aspx?p=1893065.
Walser, Hans (2012): Fibonacci. Zahlen und Figuren. Leipzig: Ed. am Gutenbergplatz (Eagle, 60 : Eagle-Einblicke).
Was hat eine Muschel mit Mathematik zu tun? (2017). Online verfügbar unter https://mathematik-akademie.de/was-hat-eine-muschel-mit-mathematik-zu-tun/, zuletzt geprüft am 26.12.2018.
Yalta, Kenan; Ozturk, Selcuk; Yetkin, Ertan (2016): Golden Ratio and the heart: A review of divine aesthetics. In: International journal of cardiology 214, S. 107–112. DOI: 10.1016/j.ijcard.2016.03.166.
Images and graphical content are taken from "wikimedia commons" database and are licensed using a CC-license if not states otherwise. If no reference is granted, the content belongs to the author.
- Otherwise used Images and graphical content:
- architecture balcony building created by David Bartus (Pexels License)
- architecture balcony building created by David Bartus (Pexels License)
- Images and graphical content taken from "wikimedia commons" database:
- Leonardo da Pisa
- Baldassarre Boncompagni
- Bernardino Baldi da Urbino
- Rafael Bombelli
- Francesco Antonio Zaccaria
- Girolamo Cardano
- Guglielmo Libri
- Johann Christoph Heilbronner
- Jean Étienne Montucla
- Leonardo da Vinci
- Niccolò Tartaglia
- Luca Pacioli
- Pietro Cossali
- Giambattista Guglielmini
- Edouard Lucas
- Eugene Charles Catalan
- Giovanni Cassini
- Maurice d’Ocagne
