Über Könige, Mathematiker und unser Logo
Herzlich Willkommen zu Ihrer Gedankenreise
Das Leben von Leonardo da Pisa
Fibonacci Folgen
Über das Logo
Literatur
Herzlich Willkommen zu Ihrer Gedankenreise
Es ist mir eine besondere Freude, den ersten Beitrag unseres Blogs zu verfassen. Eine aufregende Zeit ist vergangen und ein neuer Weg liegt vor uns und wartet darauf beschritten zu werden. Um den vielen Nachfragen nach der Bedeutung unseres Konzeptes (speziell unseres Logos) gerecht zu werden und Ihnen als interessierten Leser einen faktischen Einblick in die Gedanken hinter dem Auftritt von Markus Vogl {Business & Data Science} zu geben, dient dieser erste Beitrag.
Lassen Sie sich auf eine kurze geschichtliche und mathematische Reise einladen und sich zum Reflektieren, Nachlesen und dem Studium der Mathematik, der Geschichte und deren Faszination anregen. Dieser Beitrag ist eine Hommage an das Leben und Wirken von Leonardo da Pisa (auch als Fibonacci bekannt), ohne den dieses Konzept und im Speziellen unser Logo nicht entstehen hätte können.
Das Leben von Leonardo da Pisa

Über das Leben von Leonardo da Pisa (Fibonacci) ist weit weniger bekannt, als man es sich in Anbetracht des Einflusses seiner Werke hätte wünschen können. Als Sohn des Leiters der pisanischen Handelskolonie in Bugia (Algerien), wurde Leonardo da Pisa vermutlich 1170 geboren und ist nach einem Dokument über Pensionsgewährung (1241) in Pisa 1240 verstorben (ETH-Bibliothek). Während des Aufenthaltes in Algerien sowie mehreren Orientreisen, lernte er durch seinen muslimischen Lehrer, das indisch-arabische Zahlensystem kennen. Nach seiner Rückkehr 1200 nach Pisa, veröffentlichte er 1202 den „Liber Abaci“ (arithmetische Rechenmethoden in Bezug auf indisch-arabische Zahlensysteme) als eines für die moderne Mathematik grundlegendes und für seine Zeit sehr bedeutsames Werk (ETH-Bibliothek).
Großen Einfluss auf sein Wirken nahmen die Arbeiten von Al-Khwarizmi (arabischer Mathematiker des 9. Jahrhunderts und „Namensgeber“ des Wortes „Algorithmus“) und Abu Kamil (ägyptischer Mathematiker des 9. Jahrhunderts und „Namensgeber“ des Wortes „Algebra“) sowie antike Gelehrte wie Euklid und Ptolemaios (ETH-Bibliothek).
Durch den „Liber Abaci“ sowie die geldwirtschaftliche Entwicklung hin zu bargeldlosen Zahlungsmöglichkeiten, wurde der Streit zwischen den sogenannten „Abakisten“ und den „Algoristen“ zu Gunsten der „Algoristen“ entschieden und das uns heute vertraute Zahlensystem verbreitete sich durch ganz Europa (ETH-Bibliothek).
Einige Jahre nach der Veröffentlichung traf er 1226 auf Ansinnen des kaiserlichen Philosophen Theodor von Antiochia den Kaiser Friedrich II. Dieser – im Vergleich zu teilweise analphabetischen Herrschern – hegte ein großes Interesse an der Wissenschaft (Rader 2010). Der Hofmathematiker Johannes von Palermo, wusste zugleich Leonardo da Pisa um einige komplexe mathematische Aufgaben zu bemühen, welche Fibonacci in den Werken „Flos“ und „Liber Quadrotorum“ veröffentlichte. Diese brachten Friedrich II. ein kleines Stück näher an geistige Hochzentren, wie jene von Alfons X. el Sabio von Spanien, Sohn Ferdinands des Heiligen und Enkel Philipps von Schwaben (Rader 2010).
Die uns heute durch die „Kanninchenaufgabe“ wohl bekannte „Fibonacci-Folge“, wurde 1877 von François Édouard Anatole Lucas nach Fibonacci benannt (ETH-Bibliothek). Die Arbeiten von Leonardo da Pisa haben historisch großen Einfluss ausgeübt, den wir bis heute in unsere moderne und hoch technische Welt vernehmen können. Einen kurzen Abriss über die historische Auswirkung in der Renaissance sowie im 18./19. Jahrhundert zeigt folgende Auflistung (ETH-Bibliothek; Rader 2010):













In unserer gelebten Gegenwart finden sich Erkenntnisse und Anwendungen aus den Werken Leonardo da Pisa nicht nur in den Naturwissenschaften, sondern untern anderem auch in Grafikdesign und auf den Finanzmärkten (u.a. Elliot-Wellen-Theorie, Fibonacci-Retracements) wieder (Roller 2015).
Fibonacci Folgen
Obwohl Leonardo da Pisa und seine Werke einen maßgeblichen Einfluss auf die modernen Wissenschaften ausgeübt haben, ist weltweit seine wohl bekannteste Konzeption (egal ob formal oder graphisch) die sogenannte Fibonacci Folge. Die Fibonacci Zahlenfolge, ist eine mathematische Folge nicht negativer, ganzer Zahlen, welche bis auf die ersten beiden Elemente einem rekursiven Bildungsgesetz folgt (Roller 2015).
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, … ist der Beginn der Fibonacci Folge, bei der jedes Element (mit Außnahme der ersten zwei Zahlen) die Summe der vorherigen Elemente darstellt. Die n – te Fibonacci- Zahl wird nachfolgend als f_{n} bezeichnet und kann wie folgt dargestellt werden (Walser 2012):
f_{n}= \begin{cases} 0 & \text{ for } n = 0 \\ 1 & \text{ for } n \in \left \{ 1, 2 \right \}\\ f_{n-1}+f_{n-2} & \text{ for } n \geq 3 \end{cases}
Erweiterungen dieser Folge für negative Indices, eröffneten Möglichkeiten in multiplen und diversen Forschungs- und Anwendungsfeldern (u.a. Verallgemeinerungen auf komplexe Zahlen, proendliche Zahlen, Vektorräume) und kann folgendermaßen veranschaulicht werden (Walser 2012):
f_{0}= 0
f_{-n}= \left ( -1 \right )^{n+1}f_{n}
Im Folgenden widmen wir uns den Teilbarkeiten sowie dem bekannten Namen des goldenen Schnitt, welcher sehr oft mit oben genannter Fibonacci Folge verbunden wird. Betrachtet man die Teilbarkeiten der Elemente und den Zusammenhang mit den Indices der Folge kann aufgezeigt werden, dass das Element einer geraden Zahl entspricht, sofern der Index durch 3 dividierbar ist (Vorob’ev 2013).
In folgender Tabelle werden einige (nicht abschließende) Teilbarkeiten dargestellt.
Die Tabelle versteht sich, als dass die Teilbarkeit eines Elementes durch die aufgeführte Zahl gegeben ist, sofern die Indexnummer des selbigen Elementes durch die angegebene Zahl teilbar ist (z.B. ist eine Zahl der Fibonacci Folge durch 3 teilbar, sofern der Index durch 4 teilbar ist) (Vorob’ev 2013).
| Teilbarkeit Element | Teilbarkeit Index |
|---|---|
| 3 | 4 |
| 4 | 6 |
| 5 | 5 |
| 7 | 8 |
| 16 | 12 |
Taucht man nun etwas tiefer in die Teilbarkeiten, liegt der Gedanke, das Verhalten der Elemente untereinander näher zu betrachten, nicht fern. Betrachten wir die Verhältnisse der Zahlen der Fibonacci Folge, so stellt sich heraus, dass es für die Quotientenformel \frac{f_{n}}{f_{n-1}} einen Grenzwert gibt, welcher folgendermaßen dargestellt werden kann (Walser 2012):
\varphi = \lim_{n \to \infty }\frac{f_{n-1}}{f_{n}}
Dieser Grenzwert, stellt die Verhältnisse eines Elementes zum nächst kleineren Element dar und konvergiert gegen 0,6180… (Roller 2015).
Es ist jedoch durchaus möglich den Grenzwert der Verhältnisse eines Elementes zum nächst größeren Element darzustellen, welcher gegen 1,6180… und somit gegen den von Johannes Kepler benannten goldenen Schnitt konvergiert (Roller 2015):
\Phi = \lim_{n \to \infty }\frac{f_{n+1}}{f_{n}}
Einige interessante Eigenschaften sind, dass \varphi der Kehrwert von \Phi ist und der Grenzwert sich bei Verhältnissen zu den jeweils übernächsten Elementen verdoppelt restriktive halbiert (Roller 2015).
Da nun die grundlegenden Eigenschaften und Teilbarkeiten der Fibonacci-Folgen beschrieben wurden, können wir uns den Identitäten der Folge widmen, welche hier nur kurz angerissen werden sollen, bevor uns die Reise einige spannende Erkentnisse bringt (Walser 2012):




Identitäten der Fibonacci Folge
- \large f_{m+n}=f_{n+1}f_{m}+f_{n}f_{m-1}
- \large f_{m+n}=f_{n}L_{m}+\left ( -1 \right )^{m+1}f_{n-m} wobei
\large L_{m}=f_{m+1}+f_{m-1}=\Phi^{m}+\Psi ^{m} die Lucas Identität darstellt - f_{n}^{2}-f_{n+k}+f_{n-k}=\left ( -1 \right )^{n-k}f_{k}^{2} beschreibt die Identität von Cassini
- f_{m}f_{n-1}-f_{n}f_{m+1}=\left ( -1 \right )^{n}f_{m-n} stellt die Identität von d’Ocagne dar
Wie versprochen widmen wir uns nun einigen nennenswerten und spannenden Erkentnissen über die Verwendbarkeiten und Möglichkeiten der Fibonacci Folge. Hervorzuheben ist hier der belgische Amateur-Mathematiker Edouard Zeckendorf (1901-1983), und dessen sogenanntes Zeckendorf Theorem (Knuth 1968).
Dieses sagt aus, dass jede natürliche Zahl n > 0 eindeutig als Summe voneinander verschiedenen, nicht direkt aufeinander folgenden Elementen der Fibonacci Folge f_{j} gebildet werden kann (Knuth 1968). Daher existiert eine (eindeutige, aufsteigende) Sequenz \left ( c_{j} \right )_{i=0}^{k} so dass c_{j}\geq 2 und c_{j+1}> c_{j}+1 für j\geq 2 und n = \sum_{j=0}^{k}f_{c_{j}} gilt (Knuth 1968).
Um obiger Ausführung den abstrakten Charakter zu nehmen, stelle man sich vor, man möge die Zahl n = 3 mittels des Zeckendorf Theorems beschreiben, was mittels der Verwendung von f_{2+2} als beschreibende Funktion möglich wird (Knuth 1968).
Obige Darstellung beschreibt, wie man natürliche Zahlen mittels der Fibonacci Folge bilden kann. Im Folgenden gehen wir näher auf ein Bildungsgesetz ein, welches bereits Leonhard Euler und Daniel Bernoulli (dieser lieferte später den mathematischen Beweis) ein Begriff war. Mittels des Bildungsgesetzes von Abraham de Moivre und Jacques Phillippe Marie Binet können die Glieder der Folge direkt gebildet werden (Walser 2012).
In Matrixform sieht dies folgendermaßen aus (Walser 2012):
F = \left (\begin{matrix} 1 &1 \\ 1 & 0 \end{matrix} \right )^{n} = \left ( \begin{matrix} f_{n+1} & f_{n}\\ f_{n}& f_{n-1} \end{matrix} \right )
Besonders hervorzuheben ist der Eigenwert von F, welcher dem goldenen Schnitt entspricht und dessen Kehrwert zur oben genannten Binet Formel führt (Walser 2012).
Die Konzepte mögen theoretisch und abstrakt wirken, haben aber auch praktische Indikationen. Neben der Biologie, Physik und anderen naturwissenschaftlichen Disziplin, der quantitativen Finanzmarktanalyse, finden diese auch in der Informatik Einzug (Knuth 1968). Hier sind Fibonacci-Bäume (auch AVL-Bäume) sowie Fibonacci-Heaps (als Spezialfall der AVL-Bäume) zu nennen (Fredman und Tarjan 1987).
Über das Logo
Nachdem wir uns nun ausführlich mit Leonardo da Pisa und den mathematischen Implikationen seiner Werke beschäftigt haben, ist es an der Zeit den eigentlichen Zusammenhang mit unserem Logo aufzuzeigen, welcher sicherlich nicht sofort ersichtlich ist. Diese Möglichkeit möchten wir nutzen, um Ihnen die Konstruktion und Interpretation unseres Logos näher zu bringen und Ihnen einen tieferen Einblick in Markus Vogl {Business & Data Science} zu geben.

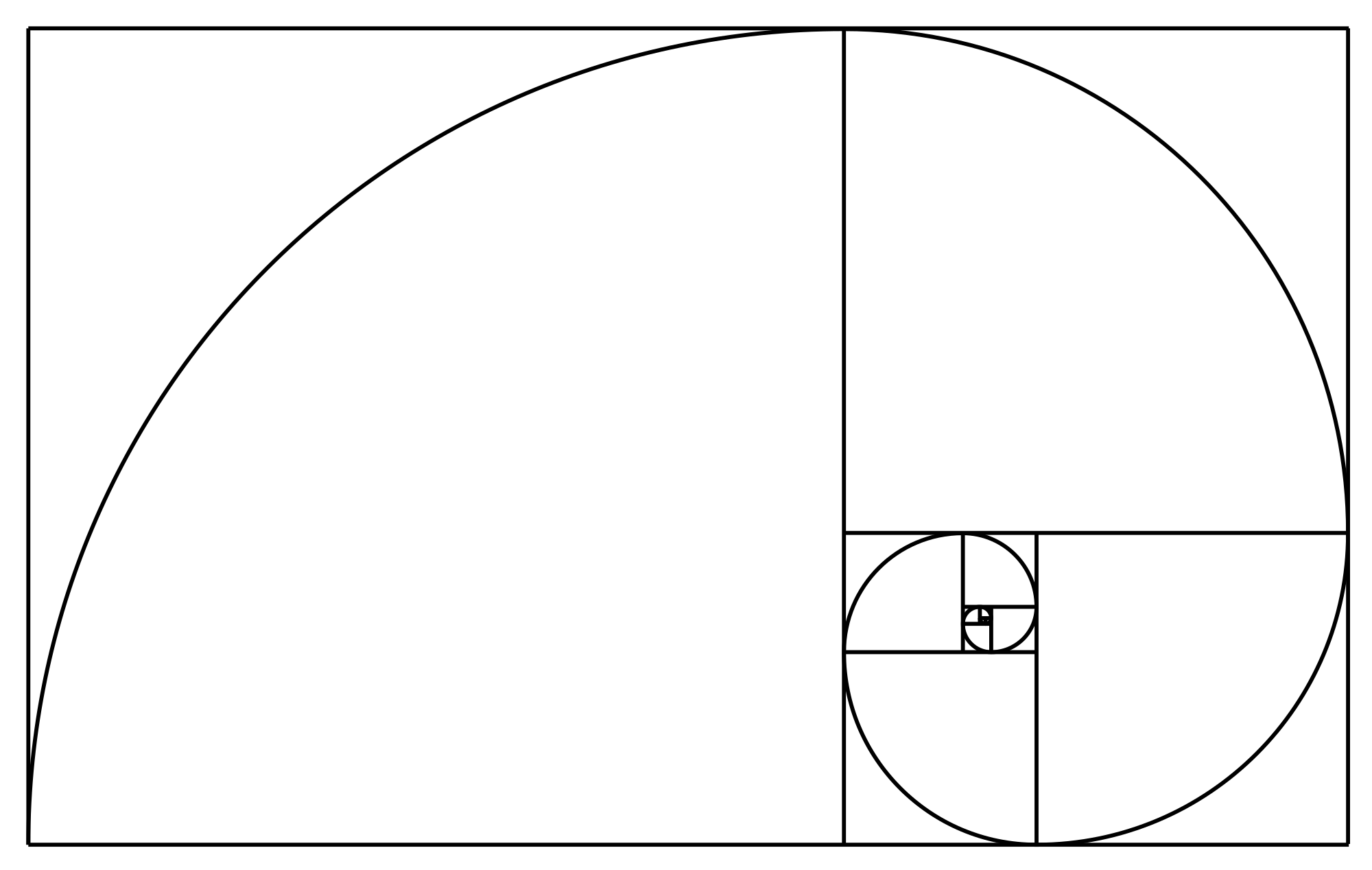
Wie aus der Fibonacci Spirale und dem Konstruktionsgitter (rechts) unser Logo auf der linken Seite entsteht, zeigen wir nachfolgend auf. Das Kontruktionsgitter stellt die Fibonacci Folge grafisch dar, indem die Seitenlängen der oben rechts gezeigten Quadrate den Zahlenwerten der Elemente der Folge entsprechen. Die Spirale verbildlicht den goldenen Schnitt.
Für unser Logo wurden die Innenkreise der Quadrate der Elemente der Fibonacci Folge mit den Werten 13 und 34 sowie das Quadrat, dass dem Wert 21 der Folge entspricht verwendet (orange markiert). Diese drei grafischen Elemente werden nun ineinander zentriert.
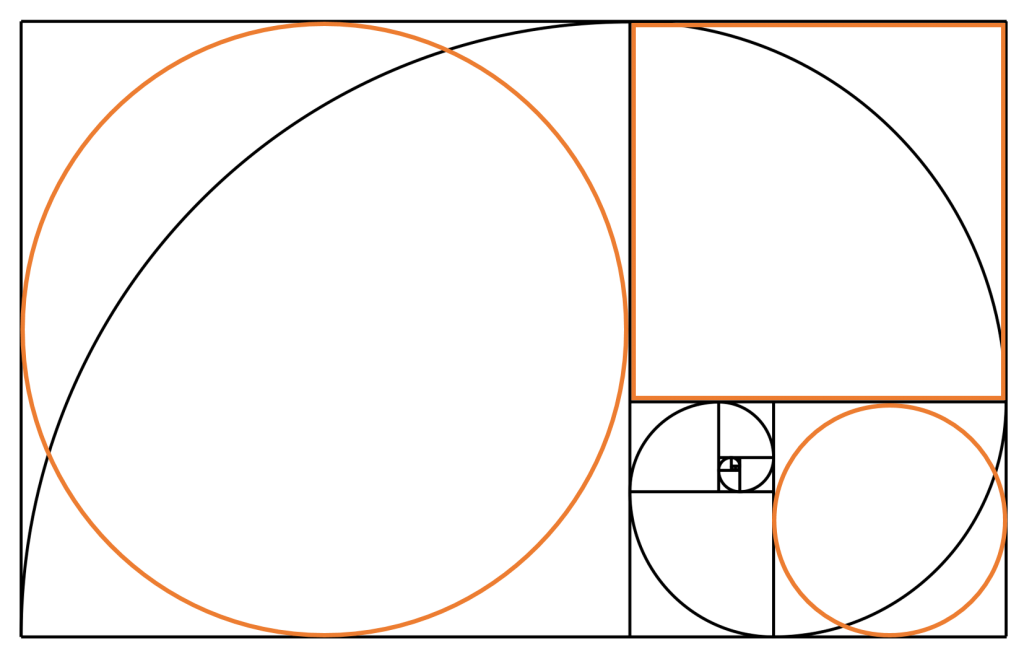

Um das Logo nun zu vervollständigen, werden Geraden eingefügt, welche durch den Schnittpunkt der Mittelpunktslinie (gestrichelte Linie) mit dem inneren Quadrat unten und durch die jeweiligen Ecken des inneren Quadrates oben verlaufen. Durch eine Verschiebung zum Schnittpunkt der Mittelpunktslinie mit dem äußeren Kreis unten, entsteht der Grundriss. Die Mittelpunktslinie im inneren Kreis wird Teil des Logos.

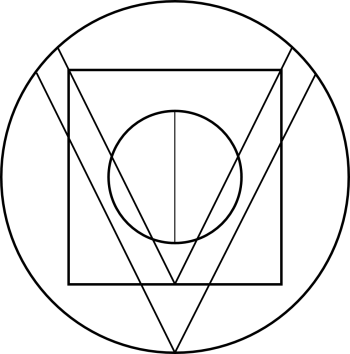
Das so entstandene Logo bietet eine große Varietät an Interpretationsspielraum und Möglichkeiten neue Wege und Muster zu entdecken. Dies ist nicht nur Sinnbild für was wir stehen, sondern auch eine Freude und Quelle der Inspiration. Einige mögliche Interpretationen und Deutungsmöglichkeiten möchten wir Ihnen hier vorstellen.
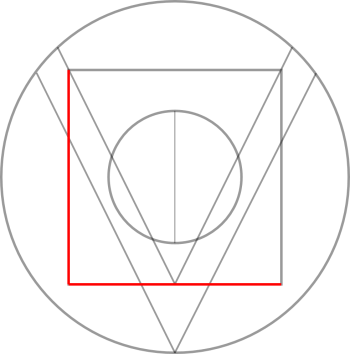
Zum einen sollte als eine Art Andacht der Künstler George Phillips Odom, Jr. (1941- 2010) und seine Werke zum goldenen Schnitt Einfluss finden, zum anderen die Initialen/der Name M.Vogl aus Markus Vogl {Business & Data Science} sich im Logo widerfinden. Geschafft haben wir beides (rot markiert), inklusive einem tatsächlichen Bild eines „Vogel“ (Ironie ist durchaus gewünscht).




In diesem Sinne freue ich mich auf Ihre Meinungen, Rückmeldungen, Anregungen und auf zukünftige Projekte.
Hochachtungsvoll,
Ihr Markus Vogl
Literatur
Benavoli, A.; Chisci, L.; Farina, A. (2009): Fibonacci sequence, golden section, Kalman filter and optimal control. In: Signal Processing 89 (8), S. 1483–1488. DOI: 10.1016/j.sigpro.2009.02.003.
ETH-Bibliothek: Biographie von Leonardo Pisano / Fibonacci. Un ponte sul Mediterraneo / Virtuelle Ausstellungen / ms / Home – ETH-Bibliothek. Online verfügbar unter http://www.library.ethz.ch/ms/Virtuelle-Ausstellungen/Fibonacci.-Un-ponte-sul-Mediterraneo/Biographie-von-Leonardo-Pisano, zuletzt geprüft am 26.12.2018.
Fibonacci-Analyse und Fibonacci-Trading: Die Know-how-Serie! Online verfügbar unter https://www.godmode-trader.de/know-how/fibonacci-analyse-und-fibonacci-trading-die-know-how-serie,5808764, zuletzt geprüft am 26.12.2018.
Fredman, Michael L.; Tarjan, Robert Endre (1987): Fibonacci heaps and their uses in improved network optimization algorithms. In: J. ACM 34 (3), S. 596–615. DOI: 10.1145/28869.28874.
Knuth, Donald Ervin (1968): The art of computer programming. Reading, Mass.: Addison-Wesley (Addison-Wesley series in computer science and information processing).
Ozturk, Selcuk; Yalta, Kenan; Yetkin, Ertan (2016): Golden ratio: A subtle regulator in our body and cardiovascular system? In: International journal of cardiology 223, S. 143–145. DOI: 10.1016/j.ijcard.2016.08.147.
Rader, O. B. (2010): Friedrich II.: der Sizilianer auf dem Kaiserthron : eine Biographie: Beck. Online verfügbar unter https://books.google.de/books?id=14iWw9uYFHwC.
Roller, K. (2015): Ichimoku-Trading: Besser traden mit der Wolkenchart-Indikatortechnik: FinanzBuch Verlag. Online verfügbar unter https://books.google.de/books?id=RyzfCQAAQBAJ.
Vorob’ev, Nikolai Nikolaevich (2013): Fibonacci Numbers. Newburyport: Dover Publications (Dover Books on Mathematics). Online verfügbar unter http://gbv.eblib.com/patron/FullRecord.aspx?p=1893065.
Walser, Hans (2012): Fibonacci. Zahlen und Figuren. Leipzig: Ed. am Gutenbergplatz (Eagle, 60 : Eagle-Einblicke).
Was hat eine Muschel mit Mathematik zu tun? (2017). Online verfügbar unter https://mathematik-akademie.de/was-hat-eine-muschel-mit-mathematik-zu-tun/, zuletzt geprüft am 26.12.2018.
Yalta, Kenan; Ozturk, Selcuk; Yetkin, Ertan (2016): Golden Ratio and the heart: A review of divine aesthetics. In: International journal of cardiology 214, S. 107–112. DOI: 10.1016/j.ijcard.2016.03.166.
Bilder und graphische Abbilder sind (sofern nicht geistiges Eigentum des Autors) aus der „wikimedia commons“- Datenbank und unterliegen einer freien CC Lizenz., oder sind unten aufgeführt.
- Verwendete Bilder und Graphiken:
- architecture balcony building von David Bartus (Pexels Lizenz)
- ancient antique art von Airin Party (Pexels Lizenz)
- Unter Verwendung historischer Bilder sowie einer CC-Lizenz (siehe oben):
- Leonardo da Pisa
- Baldassarre Boncompagni
- Bernardino Baldi da Urbino
- Rafael Bombelli
- Francesco Antonio Zaccaria
- Girolamo Cardano
- Guglielmo Libri
- Johann Christoph Heilbronner
- Jean Étienne Montucla
- Leonardo da Vinci
- Niccolò Tartaglia
- Luca Pacioli
- Pietro Cossali
- Giambattista Guglielmini
- Edouard Lucas
- Eugene Charles Catalan
- Giovanni Cassini
- Maurice d’Ocagne
