Blog-Serie: SDE – Basics II: Räume, Algebren & Maße
Definition von Stochastischen Prozessen
Maßraum & Maße
Sigma Algebra
Messraum
Wahrscheinlichkeitsraum
Filtrierung
Literatur
Definition von Stochastischen Prozessen
Herzlich Willkommen zu unserem zweiten Teil der grundlegenden Konzepte, welche für unsere Blog- Serie benötigt werden. In diesem Teil werden wir die bereits eingeführten Raumbegriffe erweitern, Instrumente zur Messung vorstellen und den Elementen von Räumen Wahrscheinlichkeiten zuordnen. Darüber hinaus starten wir mit der zentralen Hauptfrage:
Was ist ein Stochastischer Prozess?
Ein stochastischer Prozess, welcher in vielen Gebieten und Anwendungen genutzt wird, kann einfach als eine Zusammenfassung von Zufallsvariablen, welche durch eine Menge indexiert und formal durch \left \{ X\left ( t \right ) \right \}_{t\in T} , \left \{ X_{t} \right \}_{t\in T} , \left \{ X_{t} \right \}, oder \left \{ X\left ( t \right ) \right \} dargestellt ist, beschrieben werden. In anderen Worten ist jede Zufallsvariable, welche mit dem stochastischen Prozess in Beziehung steht, eineindeutig mit einem Element dessen Zustandsraumes verknüpft.
Zur Verbildlichung kann hier eine Realisation eines stochastischen Prozesses (hier ein Beispiel eines Random Walk Prozesses, welcher später Teil der Blog-Serie wird) gezeigt werden.
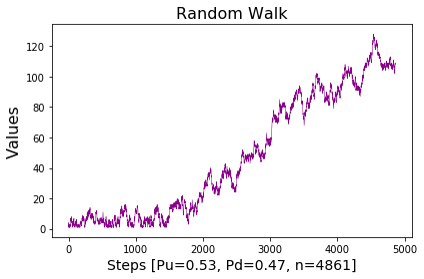
Wie wir im vorherigen Blog-Post gelernt haben, kann man einen mathematischen Raum als Menge mit gegebener Struktur betrachten.
Zustandsraum
Ein mathematischer Raum kann unter Zuhilfenahme von Ganzzahlen, reellen Linien, Euklidischen oder gar komplexen Räumen definiert werden. Werte, welche von Zufallsvariablen angenommen werden können, befinden sich („leben“) im selben mathematischen Raum, welcher nachfolgend als Zustandsraum eines gegebenen Zufallsprozesses bezeichnet wird.
Der Beitrag ist folgendermaßen aufgebaut: Anfänglich (wie im vorherigen Artikel) wird das gesamte Konzept vorgestellt. Nachfolgend wird eine mathematisch versiertere & detailliertere Vorstellung der zugrundeliegenden Konzepte und Methoden betrachtet. Nichtsdestotrotz, werden Beweise oder Komplexitäten, welche Aufgrund zu feiner Details aufkommen können vermieden und auf die gegebene Literatur verwiesen.
Zu Beginn wird eine Definition eines stochastischen Prozesses eingeführt:
Formale Definition eines Stochastischen Prozesses
Eine Zusammenfassung von Zufallsvariablen, welche über einem allgemeinen Wahrscheinlichkeitsraum \left ( \Omega ,F, P \right ) definiert sind, nennt sich stochastischer Prozess, wobei
\Omega ein Zustandsraum,
F oder \Sigma eine \sigma – Algebra und
P ein Wahrscheinlichkeitsmaß ist.
Diese Zufallsvariablen werden durch eine beliebige Menge X indexiert und nehmen Werte aus demselben mathematischen Raum S an, welche in Hinblick auf eine beliebige \sigma – Algebra messbar sein müssen. Für einen gegebenen Wahrscheinlichkeitsraum \left ( \Omega ,F, P \right ) und einen Maßraum \left ( S, \Sigma \right )
stellt ein stochastischer Prozess eine Zusammenfassung von Zufallsvariablen mit Werten aus S dar und kann folgendermaßen beschrieben werden:
\left \{ X\left ( t \right ): t \in T \right \}
wobei teinen Punkt in der Zeit Tdarstellt.
Bevor die gegebene Definition vollends verstanden werden kann, ist es notwendig Einblicke in die oben beschriebenen Formalismen zu geben. Da diese alle auf irgend eine Art und Weise miteinander verwoben sind, ist es nicht möglich diese gänzlich voneinander zu separieren. Daher haben wir uns für einen „top-down“ Ansatz entschieden, um tiefer in das Thema einzusteigen. Selbst wenn einige Teile erst später im Artikel erklärt werden, kann man sich der sorgfältigen Lektüre widmen und akzeptieren, dass einige Begriffe erst in nachfolgenden Schritten eingeführt werden. Als nächstes beginnen wir mit der Einführung sogenannter Maßräume.
Maßraum & Maße
Zu Beginn ist es von Wichtigkeit zu erwähnen, dass Maßräume von Messräumen zu unterscheiden sind. Daher, führen wir beide auch separat ein und sollten nicht verwechselt werden.
Ein Maßraum enthält Informationen über die zu Grunde liegende Menge und wird bedeutsam, sobald man an einer Beschreibung des Volumens interessiert ist. Teilmengen der zuvor genannten Menge können mittels \sigma – Algebren (welche im folgenden Teil des Artikels vorgestellt werden) und einer Methodologie für den Begriff des „Messens“, nämlich das mathematische Maß, gemessen werden. Ein Beispiel für einen Maßraum stellt der Wahrscheinlichkeitsraum dar, welcher ebenfalls erst im Folgenden vorgestellt wird.
Maßraum
Ein Maßraum ist ein Trippel \left ( X, A, \mu \right ) in dem
X eine nicht leere Menge,
A eine \sigma – Algebra auf X und
\mu ein Maß auf \left ( X, A\right )
darstellt.
Nachdem der Maßraum in irgendeiner Art mit dem Begriff “Volumen” verquickt ist, kann man zum Schluss kommen, dass man das Volumen messen kann, um Informationen zu erhalten. Intuition gibt uns vor, ein Volumen als die Ausdehnung eines beliebigen Objektes zu sehen (z.B. Menge an Luft in einem Ballon). Ein Maß auf einer Menge weist jeder geeigneten Teilmenge dieser Menge eine „Zahl“ (welche als deren Größe interpretiert) und daher als Verallgemeinerung der Konzepte von Länge, Fläche und Volumen gesehen werden kann zu.
Maß
Sei X eine Menge und \Sigma eine \sigma – Algebra über X. Eine Abbildung \mu von \Sigma auf eine reelle Linie wird Maß genannt, sofern diese folgenden Eigenschaften genügt:
- Nicht Negativität: \forall E in \Sigma :\mu \left ( E \right )\geq 0
- Nicht Leere Menge: \mu \left ( \varnothing \right )= 0
- Endliche Additivität (auch \sigma– Additivität genannt): Für alle zählbaren Zusammenstellungen \left \{ E_{j} \right \}_{j=1}^{\infty } von paarweise disjunkten Mengen in \Sigma gilt:
\mu \left ( \bigcup_{k=1}^{\infty }E_{k} \right ) = \sum_{k=1}^{\infty }\mu \left ( E_{k} \right )
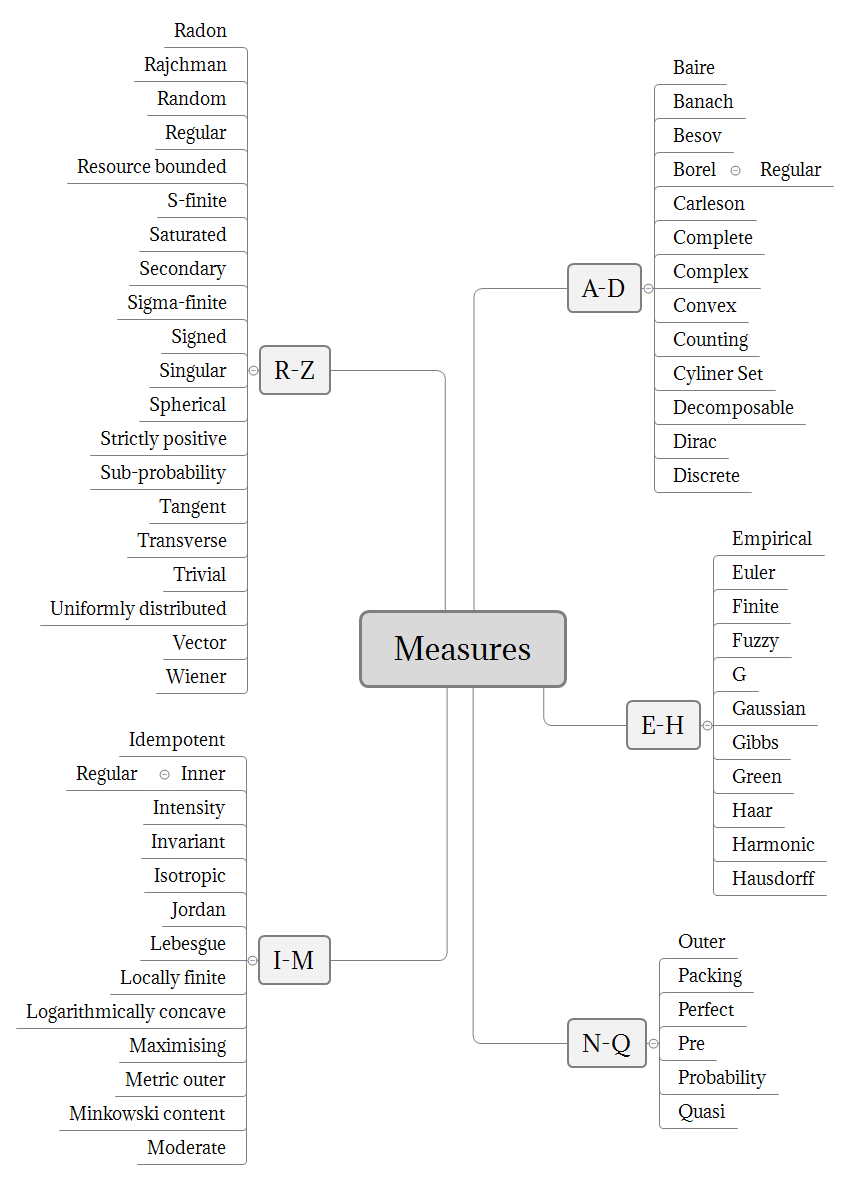
Einige der üblicherweise gebrauchten Maße sind in folgender Graphik aufgezeigt:
Im nächsten Abschnitt erläutern wir den Begriff der \sigma – Algebra , welche eine wichtige Rolle in diesem Artikel spielt.
Sigma Algebra
Im vorangegangenen Abschnitt wurde das Konzept der \sigma – Algebra öfter verwendet und es ist nun an der Zeit diese ordentlich einzuführen. Eine \sigma – Algebra gehört zur Familie der (Mengen-) Algebra oder einem sogenannten Mengensystem.
(Mengen-) Algebra
Eine (Mengen-) Algebra definiert die Eigenschaften und Regeln von Mengen, von Operationen (z.B. Berechnung) von Vereinigungen, Schnittmengen, Komplementbildung und die Beziehungen von Mengengleichheit und Verknüpfung von Mengen. Diese muss abgeschlossen sein in Hinblick auf Vereinigung und Schnittmengenbildung von endlichen Teilmengen.
Die Begriffe “Vereinigung”, “Schnitt”, “Komplement” (Grundlagen der Mengentheorie) werden nachfolgend unter zur Hilfenahme von sogenannten Venn-Diagrammen dargestellt.
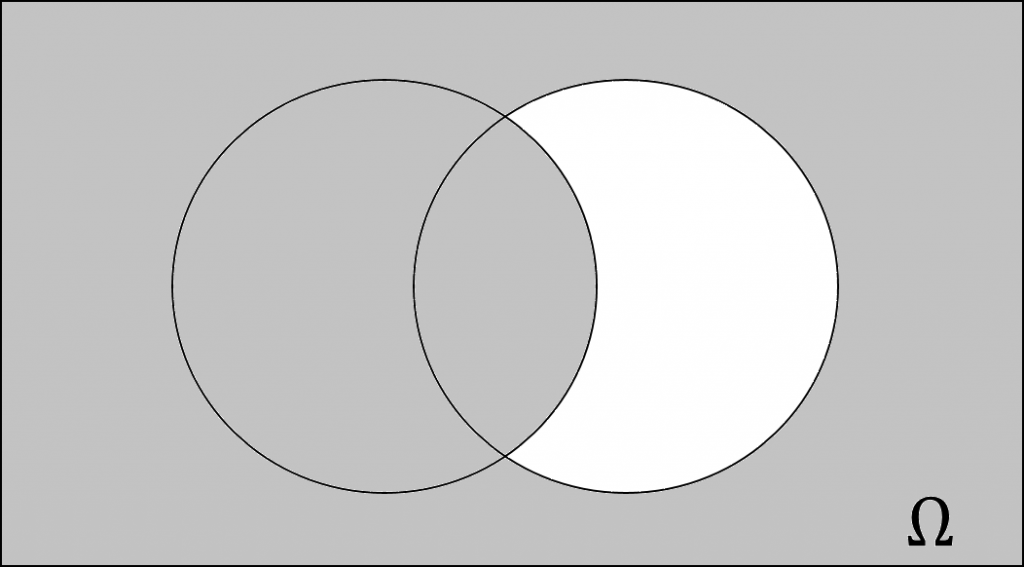
Eine \sigma – Algebra (oder \sigma – Feld) stellt eine Ausprägung einer (Mengen-) Algebra dar. Über einer Menge X ist die \sigma – Algebra eine Zusammenfassung C von Teilmengen von X , welche X selbst enthält und muss in Hinblick auf die Bildung von Komplementen und abzählbaren Vereinigungen abgeschlossen sein. Um vorherige Definition zu konkretisieren und zu vervollständigen, ist es erwähnenswert, dass die Leere Menge ebenfalls beinhaltet sein muss. Dies führt dazu, dass die \sigma – Algebra auch in Anbetracht abzählbarer Schnittmengenbildungen abgeschlossen sein muss, was im Vergleich zur (Mengen-) Algebra weit strengere Annahmen darstellt. Des Weiteren kann eine nicht leere Zusammenfassung von Mengen als \sigma – Ring bezeichnet werden. Daher kann eine \sigma – Algebra als \sigma – Ring verstanden werden, welcher die Grundgesamtheit umfasst (Ringe werden nicht weiter in diesem Artikel erläutert).
Nachdem die obige Erklärung ein wenig kryptisch klingen mag und man sich die Frage danach stellt, wie viele zu zählende Mengen überhaupt existieren mögen, ist es wichtig ein weiteres Konzept einzuführen, nämlich die sogenannte Potenzmenge.
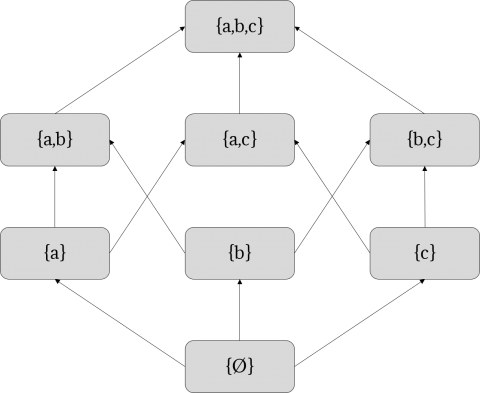
Potenzmenge
Die Menge aller Mengen einer beliebigen Menge X , welche die leere Menge und X selbst enthält (und mittels des “Weierstrass-p” gemessen werden kann) nennt sich die Potenzmenge von X .
Für eine Menge X\left \{ a, b,c \right \} verdeutlicht die folgende Graphik die Elemente der Potenzmenge von X in Hinblick auf die Eingliederung derselben.
\sigma – Algebren werden bei der Definition von Maßen genutzt (welche zuvor eingeführt wurden). Eine Zusammenfassung von Teilmengen für die ein Maß definiert wurde, ist demnach eine \sigma – Algebra.
Im Allgemeinen können Mengen, welche aus offenen oder geschlossenen Mengen aus oben genannten Operationen gebildet wurden und denen ein topologischer Raum T zugrunde liegt, als Borel Menge bezeichnet werden. Die Zusammenfassung aller Borel Mengen auf T bilden eine \sigma – Algebra (analog zu vorherigen Absatz), welche auch Borel \sigma – Algebra genannt wird und die kleinste aller möglichen \sigma – Algebren auf T darstellt, welche alle offenen (oder geschlossenen) (Teil-) Mengen auf T enthält.
Nun ist es an der Zeit eine formale Definition einer \sigma – Algebra einzuführen, um dieses Kernkonzept vollends darzustellen:
Sigma – Algebra
Sei \Omega eine Menge, dann ist eine \sigma -Algebra F auf \Omega eine Familie von Teilmengen von \Omega mit den folgenden Eigenschaften:
- \varnothing \in F
- \mathfrak{F}\in F\Rightarrow \overline{\mathfrak{F}}\in F, wobei \overline{\mathfrak{F}} = \Omega \setminus F das Komplement von F in \Omega darstellt.
- A_{1}, A_{2},… \in F \Rightarrow A:\bigcup_{j=1}^{\infty }A_{j}\in F
Um den Teil über \sigma – Algebren abzuschließen, ist es nennenswert, dass alle Elemente einer \sigma – Algebra messbar sind. Dies führt uns zum nächsten Abschnitt, den Messräumen.
Messraum
Bisher haben wir gelernt, dass man Mengen mittels \sigma – Algebren messen kann, um Informationen über diese zu erhalten. Bevor wir fortschreiten, ist es erneut sinnvoll hervorzuheben, dass Maßräume nicht mit Messräumen verwechselt werden sollten. Maßräume benötigen ein Maß, welches ein Messraum jedoch nicht erfordert.
Im Folgenden werden wir zunächst einen Messraum definieren.
Definition eines Messraumes
Das Tupel \left ( X, A \right ) nennt man Messraum, wenn
X eine nicht leere Menge und
A eine \sigma – Algebra auf X ist.
Um diese Definition zu visualisieren, ist es Wert einige gängige Messräume vorzustellen, welche in einigen Fällen auch Borel Räume genannt werden.
Wir werden nun zwei Szenarien differenzieren:
X ist endlich oder abzählbar unendlich.
In diesem Falle entspricht die entsprechende \sigma – Algebra der Potenzmenge von X . Daher gilt, A = P\left ( X \right ) und der Messraum kann als \left ( X, P\left ( X \right ) \right ) geschrieben werden.
X ist ein topologischer Raum.
In diesem zweiten Fall (wenn man zuvor die bisher vorgestellten Definitionen einer \sigma – Algebra vergleicht) entspricht die \sigma – Algebra (in den meisten Fällen) der Borel \sigma – Algebra \mathfrak{B}. Daher gilt, A =\mathfrak{B} und der Messraum kann als \left ( X, \mathfrak{B}\left ( X \right ) \right ) dargestellt werden.
Im zweiten Szenario können wir erkennen, dass topologische Räume unterschiedliche Eigenschaften aufweisen. Fortan wird der Begriff Borel Raum entweder synonym zu Messräumen oder bei Räumen, welche Borel isomorphisch zu messbaren Teilmengen in \mathbb{R} sind und zu einer Borel \sigma – Algebra führen verwendet.
Wahrscheinlichkeitsraum
Bis zu diesem Zeitpunkt haben wir sehr viel Wissen gesammelt. Nun werden wir das letzte unbesprochene Konzept erläutern, welches uns von einem vollumfänglichen Verständnis der Definition von stochastischen Prozessen am Anfang des Artikels abhält, nämlich Wahrscheinlichkeitsräume und Wahrscheinlichkeitsmaße.

Wahrscheinlichkeitsmaß
Ist ein Maß, welches nicht das Volumen oder die “Größe” misst (selbst wenn es die Eigenschaft der endlichen Additivität erfüllen muss), sondern dessen Ergebnisse auf dem Einheitsintervall \left [ 0,1 \right ] definiert sind.
Null entspricht der leeren Menge und Eins dem gesamten Raum. Im Gegensatz zu „Fuzzy“-Maßen (welche nicht Teil des Artikels sind) ist die Zuweisung des Wertes Eins zur Entsprechung des gesamten Raumes bei Wahrscheinlichkeitsmaßen verpflichtend.
Kurz gesagt, ist ein Wahrscheinlichkeitsmaß nichts anderes, als die Eintrittswahrscheinlichkeit eines Ereignisses (oder Elements), welche von Null (unwahrscheinlicher Eintritt) bis Eins (sicherer Eintritt) reicht.
Nachdem diese Wahrscheinlichkeiten ein Zuhause, beziehungsweise einen Ort zum Leben benötigen (Ironie erwünscht), sind Wahrscheinlichkeitsräume eine Notwendigkeit und werden als nächstes erläutert.
Wahrscheinlichkeitsraum
In der realen Welt (welche im Sinne dieses Artikels in weite Ferne entrückt scheint), treten Zustände (oder Szenarien, Ereignisse, Elemente) nicht deterministisch auf, sondern zufällig. Um diese zufallsgetriebene reale Welt zu modellieren, greifen Wissenschaftler und Forscher oft auf Modelle und Experimente zurück. Wenn man ein Experiment durchführt, (welches sich meist auf ein zugrundeliegendes Modell bezieht), sammeln wir Ergebnisse oder so genannte Ereignisse.
Alle Ereignisse zusammengefasst entsprechen der \sigma – Algebra F . Um festzustellen, wie wahrscheinlich der Eintritt einiger dieser Ereignisse ist, benötigt man einen Maßraum, hier einen Wahrscheinlichkeitsraum.
Ein Wahrscheinlichkeitsraum setzt sich aus drei Bestandteilen zusammen:
- Einem Ereignisraum \Omega , welcher alle möglichen Ergebnisse eines gegebenen Modelles oder Experiment enthält
- F , die \sigma – Algebra, welche einer Menge von Ereignissen entspricht (wie oben beschrieben)
- Wahrscheinlichkeiten, welche eine Indikation darüber zulassen, wie wahrscheinlich ein Ereignis eintritt oder nicht
In einem Wahrscheinlichkeitsraum wird ein einzelnes Ergebnis \omega des gesamten Ereignisraumes \Omega ausgewählt und mit den Elementen von F verglichen, um zu bestimmen ob und wenn in welchen Elementen von F dieses enthalten ist. Wird das Experiment oft genug wiederholt, kann man erkennen wie oft das Ergebnis \omega eintritt. Daher können Wahrscheinlichkeiten mittels Funktionen beschrieben werden.
Wir sind nun in der Lage einen Wahrscheinlichkeitsraum mathematisch zu definieren.
Formale Definition eines Wahrscheinlichkeitsraums
Ein Wahrscheinlichkeitsraum ist ein Maßraum in dem das Maß des gesamten Raumes den Wert 1 annimmt (wie oben beschrieben). Man kann diese Definition wie folgt erweitern:
Ein Wahrscheinlichkeitsraum ist ein Triple \left ( \Omega ,F, P \right ) bestehend aus:
- Dem Ereignisraum \Omega , welcher eine nicht leere Menge ist.
- Der \sigma – Algebra F\subseteq 2^{\Omega }, welche auch \sigma -Feld genannt wird und welche eine Menge von Teilmengen aus \Omega (auch Ereignisse genannt) darstellt, in der Form, dass:
- F den Ereignisraum enthält: \Omega \in F
- F im Hinblick auf Komplemente geschlossen ist: A \in F \Rightarrow \left ( \Omega \setminus A \right )\in F
- F im Hinblick auf abzählbare Vereinigungen geschlossen ist: A_{j} \in F für j=1,2,…, dann gilt \left ( \bigcup_{j=1}^{\infty }A_{j} \right )\in F
- In Bezug auf vorherige Punkte und der sogenannten De Morgan´s Regel (welche nicht in diesem Artikel vorgestellt wird) F im Hinblick auf abzählbare Schnitte geschlossen ist: A_{j} \in F für j=1,2,…, dann gilt \left ( \bigcap_{j=1}^{\infty }A_{j} \right )\in F
- F den Ereignisraum enthält: \Omega \in F
- Das Wahrscheinlichkeitsmaß P : F\rightarrow \left [ 0,1 \right ] stellt eine Abbildung auf F dar, in der Art, dass:
- P endlich additiv ( \sigma – additiv) ist: wenn \left \{ A_{j} \right \}_{j=1}^{\infty }\subseteq F eine abzählbare Zusammenfassung von paarweisen disjunkten Mengen ist, dann gilt P\left ( \bigcup_{j=1}^{\infty } A^{j}\right )=\sum_{j=1}^{\infty }P\left ( A_{j} \right )
- P\left ( \Omega \right )=1
- P endlich additiv ( \sigma – additiv) ist: wenn \left \{ A_{j} \right \}_{j=1}^{\infty }\subseteq F eine abzählbare Zusammenfassung von paarweisen disjunkten Mengen ist, dann gilt P\left ( \bigcup_{j=1}^{\infty } A^{j}\right )=\sum_{j=1}^{\infty }P\left ( A_{j} \right )
Alle Konzepte der ursprünglich im Artikel vorgestellten Definition sind nun formal eingeführt worden und werden ab diesem Punkt nicht tiefer, oder erneut erläutert. Zusätzlich kann man nun die Definition eines stochastischen Prozesses mit Wissen über die relevanten Begriffe erneut betrachten.
Dies schließt den Artikel bis auf den letzten Abschnitt über Filtrationen, welchen wir uns nun im finalen Teil des Artikels widmen ab.
Filtrationen
Der Einsatz von \sigma – Algebren erlaubt es uns Informationen über die zugrundeliegenden Mengen und Wahrscheinlichkeiten zu erhalten. Als Finanzanalysten sind wir an der Frage interessiert, welche Informationen zu gewissen Zeitpunkten verfügbar sind.
Eine Filtration kann daher als aufsteigende Folge von \sigma – Algebren gesehen werden, welche in Beziehung zu einem Wahrscheinlichkeitsraum und zu indexierten Mengen steht. Diese weisen eine absolute Ordnungsbeziehung auf, in der der Index Raum als T bezeichnet und gewisse Punkte in der Zeit repräsentiert.
Formale Definition einer Filtration
Sei \left ( \Omega ,A, P \right ) ein Wahrscheinlichkeitsraum und sei I eine Indexmenge mit Ordnungsrelation \leq .
Für jedes j \in I sei F_{j} eine Teil-/Unter \sigma – Algebra von A .
Demnach wird \mathbb{F}:=\left ( F_{j} \right )_{j\in I} als Filtration bezeichnet, sofern F_{k}\subseteq F_{l}\subseteq A,\forall k\leq l gilt.
Filtrationen können als Familien von \sigma – Algebren verstanden werden, welche nicht absteigend geordnet sind. Wenn \mathbb{F} eine Filtration darstellt, dann nennt man \left ( \Omega ,A,\mathbb{F}, P \right ) einen gefilterten Wahrscheinlichkeitsraum.
Filtrationen können genutzt werden um einen Überblick über die “Menge” (hier i.S.v. Anzahl, Masse an) an Informationen, welche einem stochastischen Prozess zu einem bestimmten Zeitpunkt zugrunde liegen, zu erhalten. Es wird angenommen, dass im Zeitablauf, der Informationsgehalt des Prozesses ansteigen wird.
Mit diesem Gedanken enden die Grundlagen für unsere Blog-Serie. Unser nächster Artikel wird der Agenda folgen, welche im Einführungsartikel der Serie vorgestellt wurde.
Wie immer bin ich über Feedback, Anreize und weitere Fragen sehr dankbar.
Hochachtungsvoll,
Ihr Markus Vogl
Literatur
Arens, T. et al., 2018. Mathematik. 4. Hrsg. s.l.:Springer.
Gentle, J. E. (2002). Random Walks Ch.3. In J. E. Gentle, Elements of Computational Statistics (p. 41 von 420). Springer.
Gregory F. Lawler, V. L. (2010). Random Walk: A Modern Introduction. Cambridge Studies in Advanced Mathematics, Band 123.
Haugh, M. (2010). Introduction to Stochastic Calculus. Financial Engineering: Continuous-Time Models, 18.
Horst Rottmann, B. A. (2010). Statistik und Ökonometrie für Wirtschaftswissenschaftler – Eine anwendungsorientierte Einführung. Gabler.
James L. Cornette, B. S. (2004). Random walks in the history of life. PNAS, 187–191.
Klenke, A. (2008). Probability Theory. London: Springer.
Konstantopoulos, T. (2009). MARKOV CHAINS AND RANDOM WALKS. Introductory lecture notes. University of Liverpool.
Nelson, E. (August 2001). Dynamical Theories of Brownian Motion. Princeton University Press.
Oksendal, B. (2013). Stochastic Differential Equations – An Introduction with Applications. Springer.
Peter Mörters, Y. P. (März 2010). Brownian Motion. Cambridge Series in Statistical and Probabilistic Mathematics, Band 30.
Saloff-Coste, L. (2004). Random Walks on Finite Groups. Probability on Discrete Structures , pp 263-346.
Sazonov, V. (2011, Februar 7). Encyclopedia of Mathematics. Retrieved from http://www.encyclopediaofmath.org/index.php?title=Measure&oldid=29871
Sousi, P. (October 2013). Advanced Probability. UK: University of Cambridge.
Szabados, T. (August 1994). An Elementary Introduction to the Wiener Process and Stochastic Integrals. Technical University of Budapest, 45.
Bilder und graphische Abbilder sind (sofern nicht geistiges Eigentum des Autors) aus der „wikimedia commons“- Datenbank und unterliegen einer freien CC Lizenz., oder sind unten aufgeführt.
Verwendete Bilder und Graphiken:
- abstract painting art artistic von Anni Roenkae (Pexels Lizenz)
